Perkembangan ilmu matematika tidak pernah berhenti, hal ini karena matematika masih dibutuhkan dalam kehidupan manusia. Sebelum mempelajari matematika lebih dalam, alangkah baiknya untuk mengetahui pengertian matematika menurut para ahli. Pengertian matematika tersebut dapat dijadikan sebagai acuan dasar untuk mempelajari matematika yang lebih dalam. Berikut pengertian matematika menurut para ahli, antara lain :
Pengertian Matematika Menurut Para Ahli
- Kurikulum 2004 Matematika ialah bahan kajian yang mempunyai suatu objek abstrak serta dibangun dengan melalui proses penalaran deduktif, yaitu kebenaran suatu konsep yang diperoleh sebagai akibat logis dari suatu kebenaran yang sebelumnya diterima sehingga memiliki keterkaitan antara konsep yang ada dalam matematika bersifat sangat kuat serta jelas.
- Kurikulum 2006 Matematika adalah ilmu universal yang mendasari dari perkembangan teknologi modern saat ini, memiliki peran yang penting dalam berbagai disiplin serta untuk memajukan daya pikir manusia. Perkembangan pesat pada bidang teknologi informasi serta komunikasi saat ini dilandasi karena perkembangan matematika pada bidang teori bilangan, analisis, teori peluang, aljabar, serta diskrit. Agar dapat menguasai serta untuk menciptakan teknologi pada masa yang akan datang, maka diperlukan penguasaan dibidang matematika yang kuat sejak dini.
- Yansen Marpaung Yansen Marpaung berpendapat bahwa ilmu matematika merupakan ilmu yang dalam perkembangan penggunaanya dengan menganut metode deduksi.
- Hudoyo Matematika berkenaan dengan ide, aturan, hubungan yang diatur dengan logis sehingga matematika memiliki keterkaitan dengan dengan konsep abstrak.
- Soedjadi Menurut Sodjadi berpendapat bahwa matematika merupakan pengetahuan yang bersifat eksak dengan objek abstrak yang meliputi prinsip, konsep, serta operasi yang ada hubungannya dengan suatu bilangan.
- Johnson dan Rising Matematika ialah pola berpikir, pembuktian yang logik, pola mengorganisasikan, matematika adalah suatu bahasa dengan menggunakan istilah yang dapat didefinisikan secara akurat, cermat, dan jelas, representasinya dengan simbol serta padat, lebih berupa sebuah bahasa simbol tentang ide dibandingkan tentang bunyi.
- Reys, dkk Matematika merupakan telaah mengenai pola dan juga hubungan, sebuah jalan atau pola fikir, seni, bahasa serta suatu alat.
- Kline Kline berpendapat bahwa matematika bukan merupakan pengetahuan menyendiri yang dapat menjadi sempurna karena matematika itu sendiri, melainkan dengan adanya matematika itu terutama agar dapat membantu manusia dalam mengatasi dan memahami permasalahan ekonomi, sosial, dan juga alam. Ilmu matematika tumbuh serta berkembang karena adanya proses berpikir, oleh sebab itu logika merupakan salah satu dasar agar terbentuknya matematika.
- Riedesel Riedesel berpendapat bahwa matematika ialah kumpulan dari kebenaran dan aturan, ilmu matematika bukan sekedar hanya berhitung saja. Matematika merupakan suatu bahasa, kegiatan untuk pembangkitan masalah serta untuk memecahkan suatu masalah, kegiatan untuk menemukan serta untuk mempelajari pola dan hubungan.
- Suwarsono Menurut pendapat dari Suwarsono, bahwa ilmu matematika merupakan sebuah ilmu yang mempunyai sifat khas antara lain : memakai berbagai jenis lambang yang penggunaanya tidak banyak digunakan di kehidupan sehari-hari, objeknya bersifat abstrak, serta memiliki proses berpikir yang dibatasi dengan berbagai aturan yang ketat.
- Susilo Susilo berpendapat bahwa ilmu matematika bukanlah sekedar hanya kumpulan angka, simbol, serta berbagai rumus yang tidak ada hubungannya dengan kehidupan dunia nyata. Namun sebaliknya, bahwa ilmu matematika tumbuh serta berakar dari kehidupan di dunia nyata.
- Suherman Ilmu matematika ialah disiplin ilmu mengenai tata cara berfikir serta untuk mengolah logika, baik itu secara kuantitatif ataupun kualitatif.
- James dan james Matematika merupakan suatu ilmu mengenai logika tentang bentuk, besaran, susunan, serta berbagai konsep yang memiliki hubungan satu sama lain dan dengan jumlah banyak yang terbagi ke 3 bidang, antara lain : aljabar, geometri, dan analisis.
- Abdurrahman Menurut Abdurrahman berpendapat bahwa ilmu matematika merupakan sebuah bahasa simbolis yang mempunyai suatu fungsi praktis untuk mengekspresikan berbagai hubungan kuantitatif serta keruangan, sedangkan fungsi teoritis agar dapat memudahkan berfikir.
- Andi Hakim Nasution Andi Hakim Nasution berpendapat bahwa ilmu matematika merupakan ilmu struktur, urutan (order), serta memiliki hubungan yang meliputi berbagai macam dasar pengukuran, perhitungan, serta penggambaran suatu bentuk objek.
- Ruseffendi E. T Ilmu matematika terorganisasikan dari berbagai jenis unsur yang tidak untuk didefinisikan, berbagai definisi, aksioma, serta suatu dalil dimana dalil tersebut telah dibuktikan kebenarannya dan berlaku secara umum, oleh sebab itu ilmu matematika dapat disebut sebagai ilmu deduktif.
Itulah 16 pengertian matematika menurut para ahli. Dengan pengertian matematika menurut para ahli tersebut dapat dijadikan sebagai acuan dasar untuk mempelajari matematika yang lebih dalam
Read more: http://woocara.blogspot.com/2015/12/pengertian-matematika-menurut-para-ahli.html#ixzz44JTE6n8u










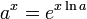
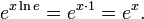
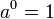
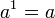
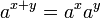
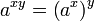

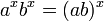
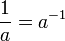
![\sqrt[n]{a^b} = \left(\sqrt[n]{a}\right)^b = a^{b/n}](https://upload.wikimedia.org/math/6/c/c/6ccd47716ad71f8a4fde5b222b912647.png)

